基本概念

明文与密文

  • Plaintext，明文，未经加密的消息，任何人都可以读
  • Ciphertext，密文，加密后的消息，不可读
  • Key，密钥，用于加密和解密（核心是算法）

加密与解密概念

加密

数据加密 的基本过程，就是对原来为 明文 的文件或数据按 某种算法 进行处理，使其成为 不可读 的一段代码，通常称为“密文”。通过这样的途径，来达到 保护数据 不被 非法人窃取、阅读的目的。

解密

加密 的 逆过程 为 解密，即将该 编码信息 转化为其 原来数据 的过程。

对称加密和非对称加密

加密算法分 对称加密 和 非对称加密，其中对称加密算法的加密与解密 密钥相同，非对称加密算法的加密密钥与解密 密钥不同，此外，还有一类 不需要密钥 的 散列算法。

Responsive Image

Responsive Image

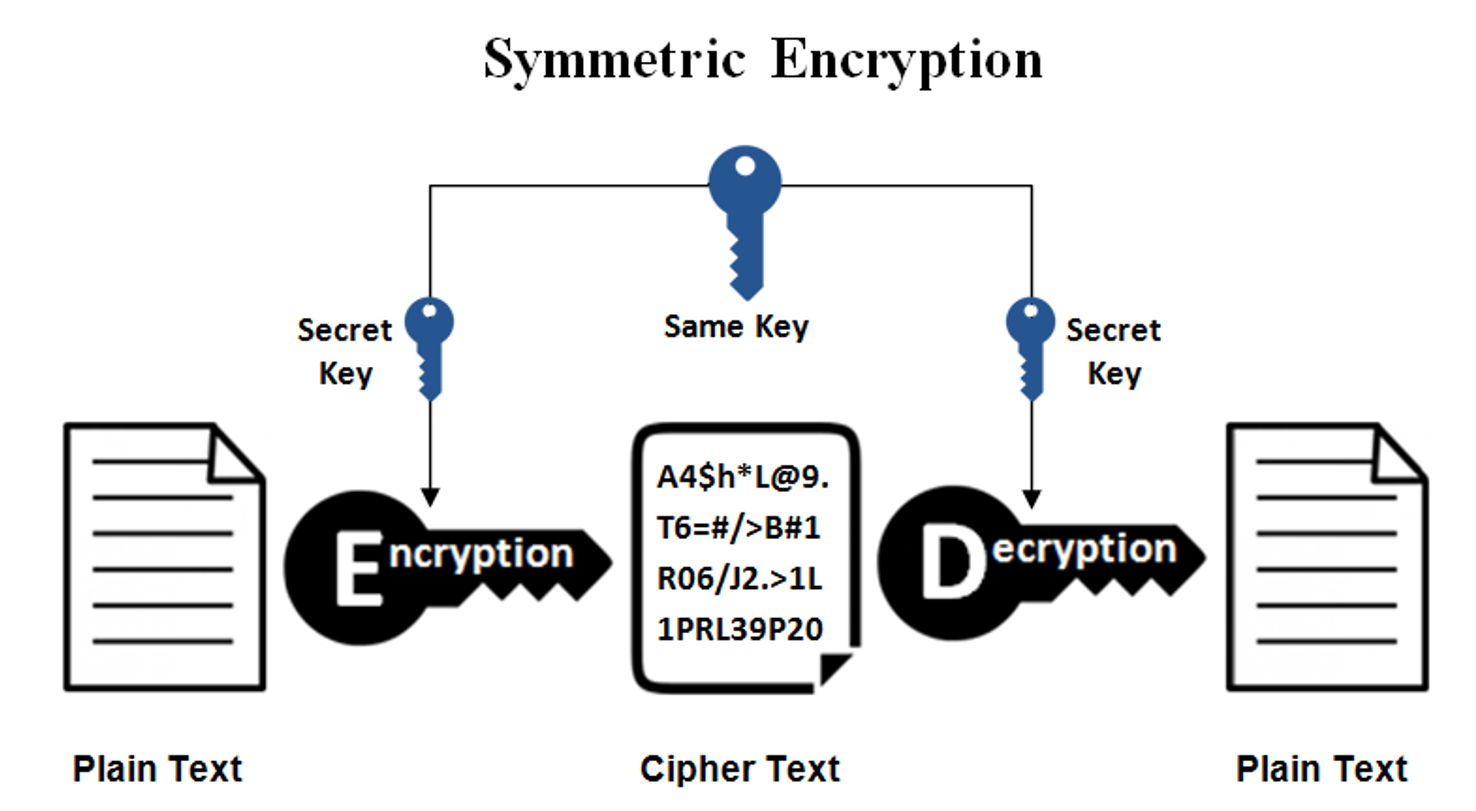
对称加密

对称加密算法 是应用较早的加密算法，又称为 共享密钥加密算法。在 对称加密算法 中，使用的密钥只有一个，发送 和 接收 双方都使用这个密钥对数据进行 加密 和 解密。这就要求加密和解密方事先都必须知道加密的密钥。

  • 数据加密过程：在对称加密算法中，数据发送方 将 明文 (原始数据) 和 加密密钥 一起经过特殊 加密处理，生成复杂的 加密密文 进行发送。

  • 数据解密过程：数据接收方 收到密文后，若想读取原数据，则需要使用 加密使用的密钥 及相同算法的 逆算法 对加密的密文进行解密，才能使其恢复成 可读明文。

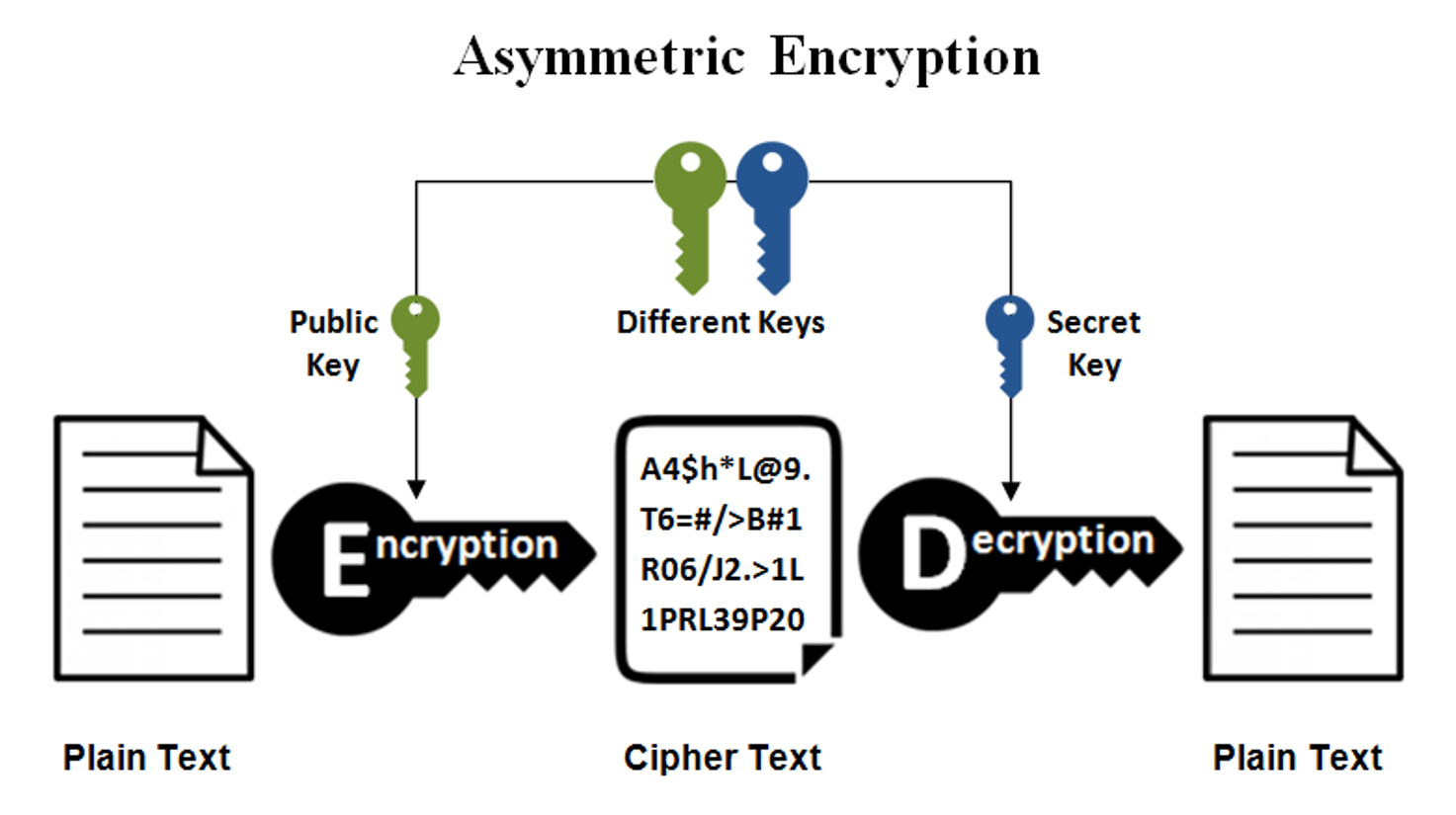
非对称加密

非对称加密算法，又称为 公开密钥加密算法。它需要两个密钥，一个称为 公开密钥 (public key)，即 公钥，另一个称为 私有密钥 (private key)，即 私钥。 因为 加密 和 解密 使用的是两个不同的密钥，所以这种算法称为 非对称加密算法。

  • 如果使用 公钥 对数据 进行加密，只有用对应的 私钥 才能 进行解密。

  • 如果使用 私钥 对数据 进行加密，只有用对应的 公钥 才能 进行解密。

数字签名

数字签名，顾名思义，就是用来证明自己身份的一种方式。在使用非对称加密算法通信时，如何验证发送者是真实的发送者，发送的信息没有篡改，就需要数字签名。一套 数字签名 通常定义两种 互补 的运算，一个用于 签名，另一个用于 验证。分别由 发送者 持有能够 代表自己身份 的 私钥（私钥不可泄露），由 接受者 持有与私钥对应的 公钥，能够在 接受 到来自发送者信息时用于 验证 其身份。

加密算法详解

通过以上简介可以了解到，加密算法分为需要秘钥的和不需要秘钥的，需要秘钥的有可以分为对称加密与非对称加密两大类。接来来我们就详细探究一下各个加密算法。

哈希算法（不可逆）

哈希算法可以将任意长度的输入数据，生成固定长度的输出（哈希值）。

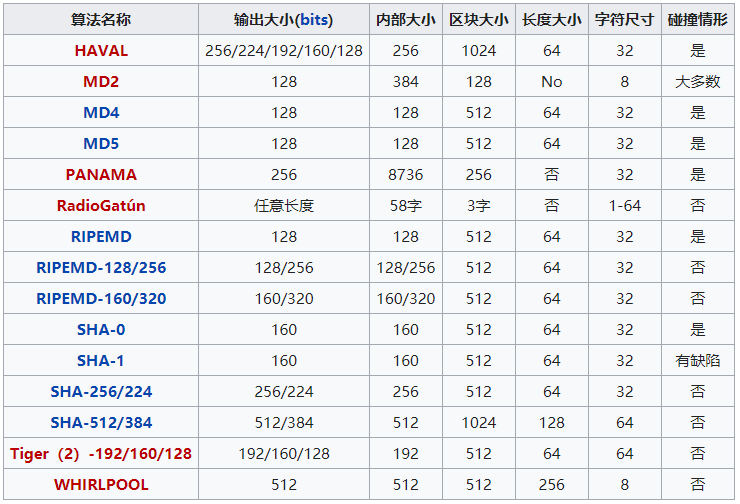
常见的哈希算法有如下：

Responsive Image

目前比较常用的是 MD5 和 SHA 系列（比如比特币用的 SHA256 算法，Git 中的 commit hash 用的 SHA1）。

MD5

MD5（Message-Digest）典型应用是对一段信息产生 信息摘要，以 防止被篡改。严格来说，MD5 不是一种 加密算法 而是 摘要算法。无论是多长的输入，MD5 都会输出长度为 128bits 的一个串 (通常用 16 进制 表示为 32 个字符)。

SHA1

SHA1(Secure Hash Algorithm) 是和 MD5 一样流行的 消息摘要算法，然而 SHA1 比 MD5 的 安全性更强。对于长度小于 $2 ^{64}$ 位的消息，SHA1 会产生一个 160 位的 消息摘要。

对称加密（可逆）

对称加密算法是应用比较早的算法，在数据加密和解密的时用的都是同一个密钥，这就造成了密钥管理困难的问题。常见的对称加密算法有 DES、3DES、AES128、AES192、AES256。

A5/1、A5/2及RC4

A5/1、A5/2及RC4他们都属于对称加密算法，并都属于流加密。先了解什么是流加密。

在密码学中，流加密（英语：Stream cipher），是一种对称加密算法，加密和解密双方使用相同伪随机加密数据流（pseudo-random stream）作为密钥，明文数据每次与密钥数据流顺次对应加密，得到密文数据流。实践中通常把信息中的每一位跟密钥流的每一位进行异或 (xor) 运算来获得密文。

DES

DES(Data Encryption Standard) 是对称加密算法领域中的典型算法，是一种块加密算法(Block cipher)，其密钥默认长度为 56 位。块加密或者叫分组加密，这种加密方法是把明文分成几个固定大小的 block 块，然后分别对其进行加密。

DES 加密算法是对 密钥进行保密，而 公开算法，包括加密和解密算法。这样，只有掌握了和发送方 相同密钥 的人才能解读由 DES 加密算法加密的密文数据。因此，破译 DES 加密算法实际上就是 搜索密钥的编码。对于 56 位长度的 密钥 来说，如果用 穷举法 来进行搜索的话，其运算次数为 $2 ^{56}$ 次。

AES

AES 是美国国家标准技术研究所 NIST 旨在取代 DES 的 21 世纪的加密标准。AES 是块加密算法，也就是说，每次处理的数据是一块（16 字节），当数据不是 16 字节的倍数时填充，这就是所谓的分组密码（区别于基于比特位的流密码），16 字节是分组长度。AES 共有 ECB、CBC 等多种模式。

SM4

SM4 算法于 2012 年被国家密码管理局确定为国家密码行业标准，最初主要用于 WAPI (WLAN Authentication and Privacy Infrastructure) 无线网络中。SM4 算法的出现为将我国商用产品上的密码算法由国际标准替换为国家标准提供了强有力的支撑。随后，SM4 算法被广泛应用于政府办公、公安、银行、税务、电力等信息系统中，其在我国密码行业中占据着极其重要的位置。类似于 DES、AES 算法，SM4 算法也是一种分组密码算法。

非对称加密（可逆）

学习非对称加密之前，我们得了解如何进行安全高效地秘钥交换。我们不可能说通信双方在通信之前，先见个面协商一下秘钥 key，这样非常不方便，但是又不能直接把 key 秘钥通过一个不安全的信道发出去，这样就会被攻击者截获。

所以我们需要有一种方法，可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容，这就是秘钥交换的概念（key exchange）。

Diffie–Hellman key exchange

迪菲-赫尔曼密钥交换（英语：Diffie–Hellman key exchange，缩写为 D-H）是一种安全协议。可以完成上述秘钥交换。

Responsive Image

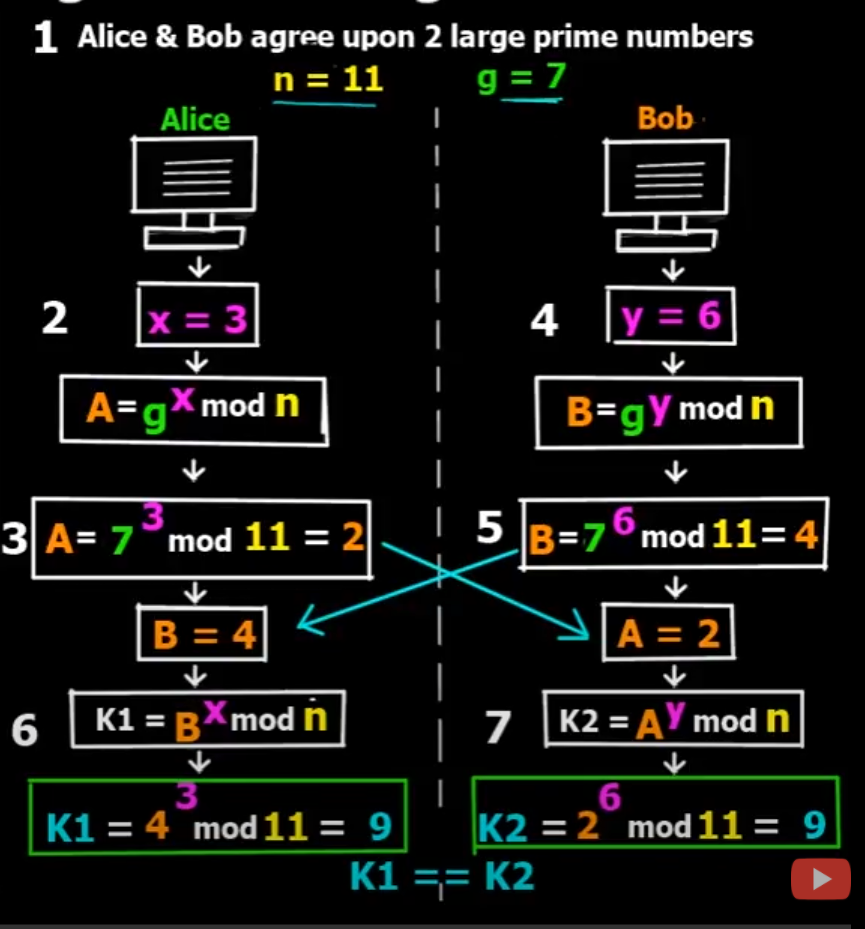
  1. 通信双方 Alice 和 Bob 个准备一个大的质数，Alice 准备的质数是n=11, Bob 准备的质数是g=7，n和g是公开的，任何第三方都可以获取到这个信息。

  2. Alice 准备一个随机自然数x=3, 除了 Alice 没有人知道x是多少，Alice 通过计算g的x次方并且对 n 取模，得到结果大 A

  3. Alice 把计算得到的结果 A=2 发送给 Bob，这个信息是公开的，任何人可以获取到 A

  4. Bob 同样准备一个随机自然数 y=6，除了 Bob 没有人知道 y 是多少，Bob 通过计算 g 的 y 次方并且对 n 取模，得到结果大 B

  5. Bob 把计算结果 B=4，发送给 Alice，，这个信息是公开的，任何人可以获取到 B

  6. Alice 拿到 B 以后，对 B 求 x 次方并对 n 取模，得到 K1=9

  7. Bob 拿到 A 以后，对 A 对 y 次方并对 n 取模，得到 K2=9

K1 == K2，Alice 和 Bob 可以使用 K1，K2 作为 Key 进行通信加密。

在整个通信过程中，攻击者是无法知道 x，y 以及 K1，K2 的，或者说计算的困难很大，感兴趣的同学可以在网上找到具体的数学问题，离散对数问题的求解。

RSA

Diffie–Hellman key exchange 发明后不久出现了 RSA，另一个进行公钥交换的算法。它使用了非对称加密算法。

RSA 加密算法是目前最有影响力的 公钥加密算法，并且被普遍认为是目前 最优秀的公钥方案 之一。RSA 是第一个能同时用于 加密 和 数字签名 的算法，它能够 抵抗 到目前为止已知的 所有密码攻击，已被 ISO 推荐为公钥数据加密标准。

RSA 所用到的数学原理可以参考阮一峰老师的文章RSA 算法原理（一），文章介绍了 RSA 用到的一些数学定理，不涉及证明，这对于了解 RSA 也就足够了。

简单介绍一下秘钥是生成过程（摘自RSA 算法原理（二））：

  1. 随机选择两个不相等的质数 $p$ 和 $q$。爱丽丝选择了$61$和$53$。（实际应用中，这两个质数越大，就越难破解。）

  2. 计算$p$和$q$的乘积$n$。爱丽丝就把 $61$ 和 $53$ 相乘。 $$n = 61×53 = 3233$$

    $n$ 的长度就是密钥长度。$3233$ 写成二进制是 $110010100001$，一共有 $12$ 位，所以这个密钥就是 $12$ 位。实际应用中，RSA 密钥一般是 $1024$ 位，重要场合则为 $2048$ 位。

  3. 计算 $n$ 的欧拉函数$\varphi(n)$。根据公式： $$\varphi(n) = (p-1)(q-1)$$

    爱丽丝算出$\varphi(3233)$ 等于 $60×52$，即 $3120$。

  4. 随机选择一个整数 $e$，条件是 $1< e < \varphi(n)$，且 $e$ 与$\varphi(n)$ 互质。 爱丽丝就在 $1$ 到 $3120$ 之间，随机选择了 $17$。（实际应用中，常常选择 $65537$。）

  5. 计算 $e$ 对于$\varphi(n)$ 的模反元素 $d$。

    所谓"模反元素"就是指有一个整数 $d$，可以使得 $ed$ 被$\varphi(n)$ 除的余数为 $1$。

    $$ed ≡ 1 (mod \varphi(n))$$ 这个式子等价于

    $$ed - 1 = k\varphi(n)$$

    于是，找到模反元素 $d$，实质上就是对下面这个二元一次方程求解。

    $$ex + \varphi(n)y = 1$$

    已知 $e=17$, $\varphi(n)=3120$，

    $$17x + 3120y = 1$$

    这个方程可以用扩展欧几里得算法求解，此处省略具体过程。总之，爱丽丝算出一组整数解为 $(x,y)=(2753,-15)$，即 $d=2753$。

    至此所有计算完成。

  6. 将 $n$ 和 $e$ 封装成公钥，$n$ 和 $d$ 封装成私钥。

    在爱丽丝的例子中，$n=3233$，$e=17$，$d=2753$，所以公钥就是 $(3233,17)$，私钥就是$3233, 2753）$。

    实际应用中，公钥和私钥的数据都采用 ASN.1 格式表达。

RSA 算法为何是可靠的呢？因为该算法基于一个十分简单的数论事实：将两个大素数相乘十分容易，但想要对其乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

回顾上面的密钥生成步骤，一共出现六个数字：

$$p,q,n,\varphi(n),e,d$$

这六个数字之中，公钥用到了两个（$n$和$e$），其余四个数字都是不公开的。其中最关键的是$d$，因为$n$和$d$组成了私钥，一旦$d$泄漏，就等于私钥泄漏。

那么，有无可能在已知$n$和$e$的情况下，推导出$d$？

  • $ed≡1 (mod φ(n))$。只有知道$e$和$φ(n)$，才能算出$d$。
  • $φ(n)=(p-1)(q-1)$。只有知道$p$和$q$，才能算出$φ(n)$。
  • $n=pq$。只有将$n$因数分解，才能算出 $p$ 和 $q$。

结论：如果 $n$ 可以被因数分解，$d$ 就可以算出，也就意味着私钥被破解。

可是，大整数的因数分解，是一件非常困难的事情。目前，除了暴力破解，还没有发现别的有效方法。

举例来说，你可以对 3233 进行因数分解（61×53），但是你没法对下面这个整数进行因数分解。

12301866845301177551304949
58384962720772853569595334
79219732245215172640050726
36575187452021997864693899
56474942774063845925192557
32630345373154826850791702
61221429134616704292143116
02221240479274737794080665
351419597459856902143413

它等于这样两个质数的乘积：

33478071698956898786044169
84821269081770479498371376
85689124313889828837938780
02287614711652531743087737
814467999489
　　×
36746043666799590428244633
79962795263227915816434308
76426760322838157396665112
79233373417143396810270092
798736308917

事实上，这大概是人类已经分解的最大整数（232 个十进制位，768 个二进制位）。比它更大的因数分解，还没有被报道过，因此目前被破解的最长 RSA 密钥就是 768 位。

签名与证书

参考

  1. Learn Cryptography
  2. 浅谈常见的七种加密算法及实现 - 掘金
  3. RSA 算法原理（一） - 阮一峰的网络日志
  4. RSA 算法原理（二） - 阮一峰的网络日志
  5. 加密解密 - 面试官：说一下你常用的加密算法_个人文章 - SegmentFault 思否